netSCHOOL AUFGABEN zu Differential-/Integralrechnung
[  I N H A L T  ]     [ MATHEMATIK Übersicht ]

Aufgaben zu
13. Winkelfunktionen
13.7 Lineare Approximation der sin-Funktion

  1. Bestimme die Ableitung der cos-Funktion nach 13.7.

13.8 Die Ableitung weiterer Winkelfunktionen und ihrer Umkehrung

  1. Beweise
                arccot ' y  =  -  1
    1 + y²

  2. Leite ab
    a.   y = 3 sin 2 x             b.   y = - 2 cos ( 3 x + )             c.   y = sin² x
    d.   y = cos² x   e.   y = cosn (x)   f.   y = tan² x
    g.   y = tan 3 x²   h.   y = tan² ( cos x )   i.   y = cot ( 3 x + 5 )
    k.   y =   l.   y = 3 x + tan 3x   m.   y = 2 sin² 3x
    n.   y = sin³ x/3 - 3 sin x/3   o.   y = x² sin x   p.   y = x tan x

  3. Leite ab
    a.   y = arcsin x/2
    b.   y = 1/3 arctan x/3
    c.   y = arccos 2x
    d.   y = arccot 2/x + arctan x/2
    e.   y = arctan  x - 1                                                
    x + 1
    f.   y = arcsin  x - 1  
    x + 1
    g.   y = x · arcsin x +
    h.   y = x · ( arcsin x ) ² - 2 x + · arcsin x
    i.   y = x · arccos 2x -  ½

  4. Diskutiere und zeichne die Kurve mit der Gleichnung
    a.   y = sin x - sin³ x             b.   y = sin 2x + 2 cos x
    c.   y = 4 sin x +  1     d.   y =  2 sin x + 1      
    sin x sin x + 2
    e.   y = x sin x   f.   y = x + sin x

13.9 Stammfunktionen der Winkelfunktionen

  1. Berechne
    a.   sin x dx       b.   /2 sin 2x dx
    0 0
    c.   2 ( cos x + sin x ) dx   d.   2 sin² x dx         ( sin² x = ½ ( 1 - cos 2x ) )
    0 0
    e.   10 1 dx                   f.   1 1 dx                                                    
    1 + 4 x² 9 + x²
    0 0
    g.   2  dx     h.   a/2  dx  
    0 0

13.10 Reihenentwicklung von sin und cos

  1. Beweise ( 1 ) und ( 2 ) des Satzes in 13.10 .

  2. Berechne nach dem Beispiel in 13.10 mit einer Genauigkeit von 10-6:
    a.   sin 18°       b.   cos 1°       c.   sin 80°       d.   cos 162°

  3. Zeichne in ein Koordinatensystem
    a.   y = sin x ;   y = x ;   y = x - x3/6  und   y = x - x3/6 + x5/120
    a.   y = cos x ;   y = 1 - ½ x² ;   y = 1 - ½ x² + 1/24 x4

Weitere Aufgaben

  1. Welches gleichschenklige Trapez mit der Grundseite  a  und der Schenkellänge  b  hat größten Flächeninhalt?

  2. Wie groß ist der halbe Öffnungswinkel eines Kegels, der einer Kugel vom Radius  R  einbeschrieben ist und
        a.   desen Volumen         b.   dessen Mantelfläche maximal ist?

  3. Harmonische Schwingungen

    Wenn ein Körper der Masse  m , welcher an einer Schraubenfeder hängt, vertikal aus der Gleichgewichtslage entfernt wird, wirkt auf ihn eine rücktreibende Kraft, die proportional zur Auslenkung  y  aus der Gleichgewichtslage ist, allerdings der Auslenkung entgegengerichtet.

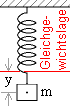
    Für die Kraft  F  gilt also
      F   = - D · y       ,
    wobei  D  eine Konstante ist, die allein von der Feder abhängt. Jede Bewegung mit diesem linearen Kraftgesetz heißt
      " harmonische Schwingung "   .
    Kraft ist gleich Masse mal Beschleunigung.
    Beschleunigung ist die 2. Ableitung der Wegfunktion  y  nach der Zeit, also  y '' (t)  . Daher ist für harmonische Schwingungen
     ( 1 )  m · y '' (t)   = - D · y (t)
    Hier liegt eine Differentialgleichnung vor. Sie stellt die Aufgabe, Funktionen  f  zu suchen, die Gleichung ( 1 ) erfüllen, d.h. für die
      m · f ''   = - D · f     ist.
    Zeige, dass  y = sin · t  die Differentialgleichnung ( 1 ) genau dann erfüllt,
    wenn     ist.
    ( heißt Kreisfrequenz.
      Es ist = 2 / T   , wobei T die Schwingungsdauer bedeutet. Damit ist
        . ) 

    Zeige, dass für dasselbe    auch die Funktionen

    1. y = cos t
    2. y = A · sin t
    3. y = A · cos t
    4. y = A · cos t  +  B · sin t     und
    5. y = A · sin ( t + )
    mit Konstanten  A  und  B  die Differentialgleichung  ( 1 )  erfüllen.
 

weitere Aufgaben zu    14. Exponential- und Logarithmusfunktionen  

 zurück zu MATHEMATIK Übersicht