Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 4.5 Symmetrische Funktionen

4.6 Beschränktheit von ganzrationalen Funktionen über Intervallen

Wir definieren zunächst:

	Die Funktion  f  heißt über der Menge  D  beschränkt,
	wenn	| f (x) | M
	für alle x D und eine positive Zahl M gilt.
Wenn die Funktionen  f  und  g  über  D  beschränkt sind, so gibt es  Mf  und  Mg  aus + , so dass
	| f(x) | Mf   und   | g(x) | Mg   über D gilt.
Dann folgt
	| f (x) + g (x) | | f (x) | + | g (x) | Mf + Mg		( Dreiecksungleichung ! )
und
	| f (x) | · | g (x) | | f (x) · g (x) | Mf · Mg

Damit ist der folgende Satz bewiesen:

Satz 4	Wenn  f  und  g  über D beschränkt sind, dann auch die Funktionen   f + g   und   f · g .

Insbesondere ist die Funktion   f (x)   über jedem Intervall [ -a | a ] durch a beschränkt ( a > 0 ).
                        | x | a
Daher sind nach Satz 4 alle Polynome über [ -a | a ] beschränkt. Man schließt nun leicht

Satz 5	Jedes Polynom ist über jedem abgeschlossenen Intervall beschränkt.

Dagegen ist z.B. das identische Polynom x x über nicht beschränkt, denn die Wertemenge ist und ist nicht beschränkt.
Vergleiche auch das Archimedische Axiom.

 
4.7 Interpolation durch ganzrationale Funktionen

Gegeben seien die Punkte
P₀ ( -2 | -4 ), P₁ ( -1 | 2 ), P₂ ( 1 | -6 ), P₃ ( 2 | -1 ), P₄ ( 5 | 20 ) .
Wir suchen eine ganzrationale Funktion kleinsten Grades, deren Kurve durch die gegebenen Punkte geht. Wir lösen die Aufgabe schrittweise.
Durch die P₀ und P₁ geht genau eine Gerade. Sie hat die Gleichung

	y = -4 + 6 ( x + 2 )	( Punkt-Steigungsform ! )
Nun suchen wir eine quadratische Parabel durch P0, P1 und P2 . Wir setzten zunächst
	y = -4 + 6 ( x + 2 ) + a2 ( x + 2 ) · ( x + 1 ) .
Die Parabel geht durch die Punkte P0 und P1 . Wir bestimmen a2 so, dass sie auch durch P2 geht:
	-6 = -4 + 6 ( 1 + 2 ) + a2 ( 1 + 2 ) · ( 1 + 1 ) .	a2 = - 10/3
Die Kurve 3. Grades
	y = -4 + 6 ( x + 2 ) - 10/3 ( x + 2 ) ( x + 1 ) + a3 ( x + 2 ) ( x + 1 ) ( x - 1 ).
geht durch die Punkte P0 ; P1 ; P2 (Probe !). Wir bestimmen a3 so, dass sie auch durch Punkt P3 geht:
	-1 = -4 + 6 · 4 - 10/3 · 4 · 3 + a3 · 4 · 3 · 1 .	a3 = 19/12
Die Kurve zu
	20 = -4 + 42 - 10/3 · 7 · 6 + 19/12 · 7 · 6 · 4 + a4 · 7 · 6 · 4 · 3	a3 = - 2/7
Die gesuchte Funktion ist also die folgende ( vom Grad 4 )
	y = -4 + 6 ( x + 2 ) - 10/3 ( x + 2 ) ( x + 1 ) + 19/12 ( x + 2 ) ( x + 1 ) ( x - 1 ) - 2/7 ( x + 2 ) ( x + 1 ) ( x - 1 ) ( x - 2 ) .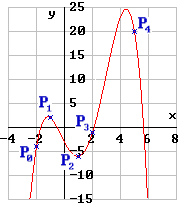

Im Aufgabenteil sind Anregungen zur Verallgemeinerung und zur Eindeutigkeit der Lösung zu finden.

weiter zu    5. Lineare Approximation  

 zurück zu MATHEMATIK Übersicht