 |
Oberstufe: Differential- und Integralrechnung
|
Oberstufenskript
Differential- und Integralrechnung
für Grund- und Leistungskurse von Jürgen Rohde |
|
 zurück zum INHALT
zurück zum INHALT |
 9.4 Die Existenz von Inhaltsfunktionen
9.4 Die Existenz von Inhaltsfunktionen
Bemerkungen
- Der Existenzbeweis ist noch nicht ganz vollständig.
Man kann ja mit einer anderen Zerlegung beginnen
und braucht auch die Verfeinerung der Zerlegung nicht unbedingt durch Halbieren vorzunehmen.
Es ist noch zu beweisen, dass jedes analoge Vorgehen zum gleichen Ergebnis führt.
Zum Beweis beachte man, dass für Zerlegungen
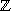 1 ,
1 ,
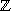 2
allgemein definiert wird
2
allgemein definiert wird
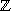 1
feiner als
1
feiner als
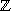 2
2
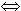
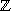 2
2
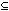
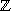 1 .
1 .
Weiter ist
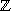 1
1

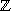 2
(kleinste) gemeinsame Verfeinerung von
2
(kleinste) gemeinsame Verfeinerung von
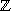 1
und
1
und
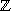 2 .
2 .
| Mit Verfeinerung nimmt |
b |
si nicht ab und |
b |
Si nicht zu. |
 |
 |
| a |
a |
Nun sei
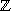 |
*
i |
eine zweite Folge von Zerlegungen von [ a | b ]
mit den Sägezahnkurven s |
*
i |
und S |
*
i |
. |
Dann sei
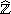 i
die Folge der Zerlegungen bestehend aus den gemeinsamen Verfeinerungen von
i
die Folge der Zerlegungen bestehend aus den gemeinsamen Verfeinerungen von
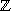 i
und
i
und
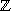 i* .
i* .
Die zugehörigen Sägezahnkurven seien
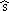 i
und
i
und
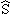 i .
i .
Aufgabe 3
| Zeige [ |
b |
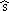 i | i | |
b |
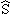 i ] i ]
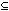 [ [ |
b |
si | |
b |
Si ]
 [ [ |
b |
s |
*
i |
| |
b |
S |
*
i |
] |
|
 |
 |
 |
 |
 |
 |
| a |
a |
a |
a |
a |
a |
| Hieraus folgt, dass alle drei Intervallschachtelungen dieselbe Zahl |
b |
f bestimmen. |
 |
| a |
- Es ist also gleichgültig, mit welcher Zerlegung man die Intervallschachtelung startet.
Besonders einfach ist häufig die Zerlegung von [ a | b ] in gleichlange Teilintervalle.
Die Länge der Teilintervalle bezeichnet man mit
 x ( = xi - xi-1 ) .
Daraus ergibt sich aus Fig. 1, dass die Summe
x ( = xi - xi-1 ) .
Daraus ergibt sich aus Fig. 1, dass die Summe
| n-1 |
f (xi) ·  x
in allen Intervallen der zugehörigen Schachtelung [ x
in allen Intervallen der zugehörigen Schachtelung [ |
b |
si | |
b |
Si ] enthalten ist. |
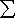 |
 |
 |
| i=0 |
a |
a |
| Das bedeutet, dass diese Summe dem bestimmten Integral |
b |
f beliebig nahe kommt, |
 |
| a |
falls  x
beliebig klein wird. Wir schreiben dafür
x
beliebig klein wird. Wir schreiben dafür
| |
|
|
|
f (xi) ·
 x = x = |
b |
f (x) dx |
|
| lim |
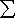 |
 |
 x x
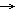 0 0 |
i |
a |
Dies ist eine für praktische Anwendungen sehr wichtige Darstellung des bestimmten Integrals.
Der Grenzwert existiert zumindest immer dann, wenn die Funktion f über
[ a | b ] L-stetig ist.
- Die Bemerkung 2 macht auch die von Leibniz eingeführte Integralschreibweise plausibel:
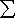 |
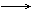 |
 |
(stilisiertes S) , f (xi) ·
 x x |
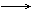 |
f (x) dx , |
worin aber f (x) und dx keine selbständige Bedeutung als Faktoren haben
und die "Variable" x nicht frei, sondern gebunden ist
Aufgaben zu 9.4
weiter zu
10. Eigenschaften L-stetiger Funktionen
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht
![]()