 |
AUFGABEN zu Differential-/Integralrechnung
|
Aufgaben 22 bis 25 zu
14. Exponential- und Logarithmusfunktionen
-
Grenzwerte im Zusammenhang mit der Eulerschen Zahl e .
-
Zeige:
Ein Kapital K wächst in einem Jahr bei p % jährlicher Verzinsung auf
| |
K1 = K ( 1 + |
p |
) |
an. |
 |
| 100 |
-
Zeige:
Werden die Zinsen halbjährlich gutgeschrieben, so wächst K in einem Jahr auf
| |
K2 = K ( 1 + |
p |
) 2 |
an. |
 |
| 2 · 100 |
-
Zeige:
Teilt man 1 Jahr in n gleichlange Zeitabschnitte
und werden die Zinsen nach jedem Abschnitt gutgeschrieben und von da ab mitverzinst,
so wächst K in 1 Jahr auf
| |
Kn = K ( 1 + |
p |
) n |
an. |
 |
| n · 100 |
-
Setzt man zur Vereinfachung K = 1 und p = 100 , so wird
| |
Kn = ( 1 + |
1 |
) n |
. |
 |
| n |
Wenn n beliebig groß wird und damit die Länge der Zeitabschnitte beliebig klein wird,
liegt es nahe, von stetiger Verzinsung zu sprechen.
Zwar spielt die stetige Verzinsung im Wirtschaftsleben keine Rolle,
wohl aber sind Wachstums- und Zerfallsvorgänge in der Natur mit diesem Begriff mathematisch zu erfassen.
Beispiele finde Sie in den folgenden Aufgaben.
-
Die Differentialgleichung y ' = k · y
Die Differentialgleichung
| ( 1 ) |
f ' (x) = k · f (x) |
|
mit k 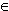 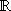 ,
k ,
k 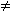 0 und f > 0 0 und f > 0 |
läßt sich so umformen:
| |
f ' (x) |
= k |
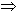 |
[ ln f (x) ] ' = k |
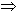 |
 |
| f (x) |
| ln f (x) = k · x + C |
( C 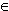  ) ) |
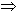 |
| f (x) = ek · x + C = |
eC · ek · x = |
f (0) · ek · x |
Zeige, dass diese Lösung richtig bleibt,
falls f (x) < 0 im Definitionsbereich von f ist.
Beispiel:
Gesucht ist die Lösung der Differentialgleichung
y ' = 3 y , welche durch den Punkt ( 0 | 2 ) geht.
Lösung: f (x) = 2 · e 3x
-
Anwendungen der Differentialgleichung y ' = k · y
-
Radioaktiver Zerfall
Das Zerfallsgesetz besagt, dass in gleichen Zeiten stets gleiche Bruchteile zerfallen.
Die Anzahl N (t) der noch nicht zerfallenen Atome eines radioaktiven Stoffes
ist also fallend und erfüllt die Differentialgleichung
| ( 1 ) |
N ' (t) = - 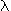 · N (t) . · N (t) . |
( Begründung ) |
| mit der Lösung |
| ( 2 ) |
N (t) = N (0) · 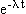 . . |
( Begründung ? ) |
Dabei heißt 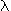 Zerfallskonstante.
N (0) ist die Anzahl der noch vorhandenen Atome zum Zeitpunkt 0 .
Wichtig ist die Halbwertszeit tH ,
in der die Hälfte der vorhandenen Atome zerfallen sind, d.h.
Zerfallskonstante.
N (0) ist die Anzahl der noch vorhandenen Atome zum Zeitpunkt 0 .
Wichtig ist die Halbwertszeit tH ,
in der die Hälfte der vorhandenen Atome zerfallen sind, d.h.
N (tH) = ½ N (0) .
| Leite aus ( 2 ) her: tH = |
ln 2 |
 |
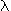 |
| Bestimme die Halbwertszeiten von |
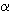 . . |
|
Plutonium 239 |
|
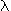 = 2,85 · 10-5 a-1
= 2,85 · 10-5 a-1 |
|
( a = Jahr ) |
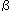 . . |
Plutonium 237 |
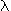 = 3,85 s-1
= 3,85 s-1 |
|
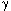 . . |
Einsteinium 254 |
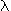 = 1,44 · 10-3 d-1
= 1,44 · 10-3 d-1 |
( d = Tag ) |
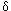 . . |
Radionuklid |
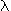 = 0,05 s-1
= 0,05 s-1 |
|
-
Die barometrische Höhenformel
Bekanntlich nimmt der Luftdruck P (h) mit der Höhe h ab.
Für P (h) gilt:
| |
P ' (h) = - |
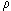 0 0 |
· g · P (h) , |
 |
| P0 |
wobei 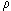 0 = 1,293 kg · m-3 ;
P0 = 105 N m-2 ; g = 9,81 m s-2 ist.
0 = 1,293 kg · m-3 ;
P0 = 105 N m-2 ; g = 9,81 m s-2 ist.
Berechne den Luftdruck in
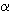 . . |
1 km |
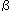 . . |
5 km |
 . . |
10 km Höhe. |
-
Einschalten eines elektrischen Gleichstromkreises
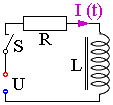 Schaltet man den nebenstehenden Stromkreis mit dem Widerstand R
und der Spule mit Eisenkern mit der Induktivität L ein,
so steigt die Stromstärke I (t) erst allmählich an.
Der zeitliche Verlauf von I wird durch die Differentialgleichung
Schaltet man den nebenstehenden Stromkreis mit dem Widerstand R
und der Spule mit Eisenkern mit der Induktivität L ein,
so steigt die Stromstärke I (t) erst allmählich an.
Der zeitliche Verlauf von I wird durch die Differentialgleichung
U - L · I ' (t) = I (t) · R
( U = konstante Gleichspannung )
beschrieben. Sie muss aber erst auf die Form y ' = k · y gebracht werden,
etwa so (Einzelschritte begründen!) :
| |
I ' (t) = |
U |
- |
R |
· I (t) = - |
R |
( I (t) - |
U |
) |
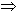 |
 |
 |
 |
 |
| L | L | L | R |
| |
[ I (t) - |
U
R |
] ' |
= - |
R |
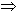 |
I (t) = |
U |
( 1 - e |
- |
R
L |
· t |
) , |
 |
 |
 |
| I (t) - |
U
R |
|
L |
R |
|
wobei beim Einschalten bei t = 0 der Strom I (0) = 0 sei.
Bestimme I (t) beim Ausschalten.
In der Differentialgleichung ist dann U = 0 und
I (0) = I0 .
Zeichne den charakteristischen Verlauf beider Kurven.
-
Setzen Sie in der Reihenentwicklung für y = ex für
x den Term - x2/2 ein.
Sie erhalten dann eine Reihe für
y = e - x2/2 .
Ohne die Rechtfertigung zu diskutieren, soll die Reihe gliedweise intergriert werden.
Man erhält eine Reihe für
| |
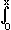 |
e |
- |
1
2 |
t2 |
dx . |
Ermitteln Sie aus der zugehöhrigen Reihe einige Funktionswerte und skizzieren Sie den Graphen der Funktion.
Diese Funktion spielt eine wichtige Rolle bei der sogenannten Normalverteilung
in der Stochastik und ist bis auf einen Faktor tabelliert.
weitere Aufgaben zu
15. Weitere Integrationsmethoden
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht
 Schaltet man den nebenstehenden Stromkreis mit dem Widerstand R
und der Spule mit Eisenkern mit der Induktivität L ein,
so steigt die Stromstärke I (t) erst allmählich an.
Der zeitliche Verlauf von I wird durch die Differentialgleichung
Schaltet man den nebenstehenden Stromkreis mit dem Widerstand R
und der Spule mit Eisenkern mit der Induktivität L ein,
so steigt die Stromstärke I (t) erst allmählich an.
Der zeitliche Verlauf von I wird durch die Differentialgleichung
![]()