 |
AUFGABEN zu Differential-/Integralrechnung
|
Aufgaben 16 bis 21 zu
14. Exponential- und Logarithmusfunktionen
-
Berechne
| |
a. |
5 |
1 |
dx |
|
b. |
5 |
( 2 + |
3 |
) dx |
|
c. |
8 |
3 |
dx |
| |
 |
 |
 |
 |
 |
 |
 |
| |
x |
x |
x - 1 |
| |
3 |
1 |
4 |
| |
d. |
3 |
5 |
dx |
|
e. |
1 |
- 2 |
dx |
|
f. |
6 |
2 x + 5 |
dx |
| |
 |
 |
 |
 |
 |
 |
 |
| |
2 x + 4 |
2 - x |
x + 2 |
| |
0 |
-2 |
1 |
| |
g. |
-½ |
3 x² + 2 x + 1 |
dx |
|
h. |
0 |
( |
1 |
+ 2 ) dx |
|
i. |
+1 |
1 |
dx |
| |
 |
 |
 |
 |
 |
 |
 |
| |
x |
x + 3 |
2 x + 3 |
| |
-3 |
-2 |
-1 |
| k. |
e |
lg x dx |
|
l. |
5 |
log2 x dx |
|
m. |
1 |
lg ( 4 x + 1 ) dx |
 |
 |
 |
| 1 |
1 |
0 |
| |
n. |
-1 |
1 |
dx |
|
o. |
1 |
1 |
dx |
|
p. |
-4 |
x |
dx |
| |
 |
 |
 |
 |
 |
 |
 |
| |
x |
2 x - 3 |
x + 2 |
| |
-3 |
-3 |
-6 |
-
Vergleiche die Kurven der Funktionen
| a. |
y = ex |
|
y = 10x |
|
y = 2x |
|
y = 0,1x |
|
y = ( ½ )x |
| b. |
y = ln x |
|
y = lg x |
|
y = log2 x |
|
y = log0,1 x |
|
y = log0,5 x |
-
Warum kann man Logarithmen mit negativen Basen nicht definieren?
-
Diskutiere und stelle wesentliche Teil der Kurve dar:
| a. |
y = x · ln x |
|
b. |
y = |
ln x
x |
|
c. |
y = |
x
ln x |
| d. |
y = x² · ln x |
|
e. |
y = |
ln sin x |
|
f. |
y = |
ln² x |
| g. |
y = ln ( 4 x - x² ) |
|
h. |
y = |
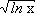 |
|
i. |
y = |
x² - ln x² |
| k. |
y = ln² x - ln x |
|
l. |
y = |
ln ( 1 + x² ) |
|
m. |
y = |
½ x² - ln x |
| n. |
y = x ( x - 2 ) · ex |
|
o. |
y = |
x · e-x |
|
p. |
y = |
e-x · sin x |
| q. |
y = ex + e-x |
|
r. |
y = |
ex - e-x |
|
s. |
y = |
x · e-x² |
| t. |
y = e- ½ x ² |
|
u. |
y = |
ex |
|
v. |
y = |
e1/x |
 |
| x² - 9 |
| w. |
y = e- | x | |
|
x. |
y = |
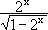 |
|
y. |
y = |
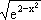 |
| |
z. |
y = |
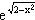 |
-
Logarithmische Ableitung
Wenn die Funktion f differenzierbar und positiv ist,
dann ist
| |
( ln f (x) ) ' = |
f ' (x) |
 |
| f (x) |
| oder |
| |
f ' (x) = |
f (x) · ( ln f (x) ) ' |
Beweise dies im einzelnen. Die Methode heißt logarithmisches Differenzieren.
Anwendungsbeispiel:
Es sei f (x) = xx .
Dann ist ln f (x) = x · ln x . ( x > 0 )
Also
| |
( ln f (x) ) ' = |
f ' (x) |
= ln x + 1 |
 |
| f (x) |
| und damit |
| |
f ' (x) = |
xx · ( 1 + ln x ) |
Bestimme analog die Ableitungen von
| a. |
y = x-x |
|
b. |
y = x1/x |
|
c. |
y = x ln x |
| d. |
y = ( 1 + x )x |
|
e. |
y = ( 1 + 1/x )x |
|
f. |
y = ( 1 + 1/x )x + 1 |
-
Logarithmische Integration
Zeige: Wenn die Funktion f über [ a | b ] differenzierbar ist
und keine Nullstelle hat, gilt
| |
 |
c · f ' (x) |
dx = c · ln | f (x) | + C |
;
c 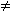 0 ,
C 0 ,
C 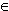 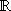 |
 |
| f (x) |
| Beispiel |
| Es sei |
y = |
3 x² |
über 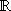 + + |
 |
| x³ + 12 |
Setzt man f (x) = x³ + 12 , so ist f ' (x) = 3 x² und
| |
 |
3 x² |
dx = ln ( x³ + 12 ) + C . |
 |
| x³ + 12 |
Die Methode der logarithmischen Integration gelingt in der Regel bei Quotienten von Funktionen,
wenn der Zähler bis auf einen konstanten Faktor die Ableitung des Nenners ist.
Bestimme Stammfunktionen zu
| a. |
y = |
x |
|
b. |
y = |
x + 1 |
|
c. |
y = |
ex - e-x |
 |
 |
 |
| x² + 1 |
x² + 2 x + 10 |
ex + e-x |
| d. |
y = |
tan x |
|
e. |
y = |
cot x |
|
f. |
y = |
ex |
 |
| ex + b |
Aufgaben 22 bis 25 zu
14. Exponential- und Logarithmusfunktionen
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht
![]()