Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 3. Das Beweisverfahren der vollständigen Induktion

4. Ganzrationale Funktionen

4.1 Wiederholung

      Übungen zur Wiederholung

 
4.2 Definition ganzrationaler Funktionen - Polynome

Jede Zuordnung x an xn + an-1 xn-1 + · · · + a2 x2 + a1 x + a0     über mit an 0 und ai heißt eine ganzrationale Funktion n-ten Grades. Der Funktionsterm (rechts vom Zuordnungspfeil) heißt Polynom n-ten Grades.
Z.B. ist   id:	x x	eine ganzrationale Funktion 1. Grades,
qu:	x x²	eine ganzrationale Funktion 2. Grades,
Pn:	x xn	(Potenzfunktion) eine ganzrationale Funktion n-ten Grades,
	x a0	a0 0 (konstante Funktion) hat den Grad Null.
Für die Nullfunktion   x 0   wird kein Grad definiert.

 
4.3 Berechnung von Funktionswerten nach dem Horner-Schema

Beispiel:	Zeichne die Funktion f mit	f (x) =	4 x³ - 21 x² + 18 x + 12 .
Die Berechnung von Funktionswerten wird einfacher und auch maschinengerechter, wenn man im Funktionsterm sukzessive ausklammert:
		f (x) =	( 4 x² - 21 x + 18 ) · x + 12
		=	[ ( 4 x - 21 ) · x + 18 ] · x + 12
	z.B. ist	f (2) =	[ ( 4 · 2 - 21 ) · 2 + 18 ] · 2 + 12
		=	[ ( 8 - 21 ) · 2 + 18 ] · 2 + 12
		=	( -13 · 2 +18 ) · 2 + 12
		=	( -8 ) · 2 + 12
		=	-4

Die Berechnung läßt sich nach folgendem Schema übersichtlicher durchführen:

	4	-21	18	12		1. Zeile: Koeffizienten des Polynoms f (x)
+		8	-26	-16		Pfeil bedeutet: mal x, hier mal 2
x = 2 |	4	-13	-8	-4	= f (2)	Pfeile werden künftig weggelassen
gewählter x - Wert
Dieses Schema heißt Horner-Schema

Die Division von f (x) durch den Linearfaktor ( x - 2 ) ergibt:

(	4 x³	- 21 x²	+ 18 x	+ 12	) : ( x - 2 ) = 4 x² - 13 x - 8 - 4 : (x - 2)
(-)	4 x³	-   8 x²
		- 13 x²
	(-)	- 13 x²	+ 26 x
			-    8 x
		(-)	-    8 x	+ 16
				-   4

(Bemerkung: Die Division von Summen ist eine Verallgemeinerung des Divisionsalgorithmus für ganze Zahlen - z.B. 1425 : 12 - und beruht wie dieser auf der Deutung der Division als Subtraktion gleicher Summanden.)

Man kann also schreiben:

	f (x) =	4 x³ - 21 x² + 18 x + 12 = -4 + ( x - 2 ) ·	( 4 x² - 13 x - 8 ) \___________________/
	=	-4 + ( x - 2 ) · g (x)	g (x)

Die Koeffizienten des Polynoms g (x) stehen in der 3. Zeile des Horner-Schemas. Also können wir uns künftig die Division sparen. Es gilt - ohne dass wir den allgemeinen Beweis durchführen -

Zu jedem Polynom n-ten Grades und zu jeder reellen Zahl x0 gibt es ein Polynom (n-1)-ten Grades g (x), so dass
	( 1 )	f (x) = f (x0) + ( x - x0 ) · g (x)
	gilt.	Die Koeffizienten von g (x) stehen in der 3. Zeile des Horner-Schemas.

Das Beispiel wird nun weiter bearbeitet. Die folgende Wertetabelle ist nach dem Horner-Schema zu überprüfen.

x	-2	-1	-0,5	0	0,5	1	2	3	3,5	4	5
f (x)	-140	-31	-2,75	12	16,25	13	-4	-15	-10,75	4	77

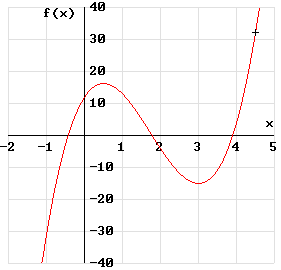
Bild von f (x) = 4 x³ - 21 x² + 18 x + 12

weiter zu    4.4 Nullstellen von Polynomen  

 zurück zu MATHEMATIK Übersicht