netSCHOOL AUFGABEN zu Differential-/Integralrechnung
[  I N H A L T  ]     [ MATHEMATIK Übersicht ]

5. Lineare Approximation

5.1 Allgemeines zum Funktionsbegriff

Aufgaben zu
5.2 Der Grundgedanke der linearen Approximation

1.Tangenten an Kreis und Normalparabel haben mit diesen nur je einen Punkt gemeinsam. Warum kann man diese Eigenschaft nicht allgemein zur Tangentendefinition benutzen?
2.Zeige: In der Definition der L-Differenzierbarkeit ist  m  nicht eindeutig bestimmt, wenn man  | R (x) |  k | x - x0 |  fordert. Beispiele !
3.Zeige: Die Forderung  | R (x) |  k | x - x0 |1/2  ist nicht sinnvoll. (vergleiche Aufgabe 2)
4.Zeige:  m  ist eindeutig bestimmt, wenn  | R (x) |  k | x - x0 |3/2  ist. (vergleiche Aufgabe 2)
5.Zeige:  x x²  ist nirgends diffenrenzierbar, wenn  | R (x) |  k | x - x0 |³  .

Aufgaben zu
5.3 Die Ableitung der ganzrationalen Funktionen

Ableitungsregeln für ganzrationale Funktionen bzw. Polynome
1.    ( xn ) ' = n · xn-1    a = Konstante
f, f1, f2, u, v
sind Funktionen
2.( a · f ) ' = a · f '
3.( f1 + f2 ) ' = f1 ' + f2 '
4.( u · v ) ' = u ' v + u v '
5.( un ) ' = n · un-1 · u '

6. Differenziere
   a)y = 4 x³ - 6 x + 5    b)y = - 2 x² + 7
c)y = - 3 x d)y = 0
e)y = 106 f)y = x2n + xn
g)y = 6 x5 - 4 x3 - 6 x2 + 3 x h)y = - 5 x8 + 6 x7 - 10 3
i)y = ( x - 1 ) · ( x² + 2 x + 8 ) k)y = ( x + 3 ) · ( x³ + 6 x - 7 )
l)y = ( x² + 6 x + 8 ) · ( x³ - 6 x + 5 ) m)y = ( x4 + 2 x - 1 ) · ( x5 + 2 x3 - 6 )
n)y = ( 2 x + 1 )4 o)y = ( - 6 x + 2 )5 · ( x + 3 )
p)y = ( 2 x² - 6 x + 15 )³ q)y = ( - 3 x³ + 6 x - 1 )4
r)y = ( 2 x² - 9 )4 · ( 3 x² + 5 x + 8 ) s)y = ( a x + b )n · ( x² - 4 )2n
t)y = ( x5 + x3 )3 · ( 6 x + 5 ) u)y = ( - 5 x² + 4 x )² · ( 3 x - 2 )³

7.Zeige: Wenn  x0   k-fache Nullstelle des Polynoms  f (x)  ist, dann ist  x0   (k-1)-fache Nullstelle des Polynoms  f ' (x) .
8.Beweise unter Voraussetzung der Produktenregel durch vollständige Induktion
 a)( xn ) ' = n · xn-1
 b)( [ u (x) ]n ) ' = n · [ u (x) ]n-1 · u ' (x)     für beliebiges Polynom  u (x)
9.Beweise durch vollständige Induktion
 a)Für alle  n     gibt es eine positive Zahl  kn , so dass für alle  x, x0  [ a b ] für das durch die Gleichung
 xn = [ x0 + ( x - x0 ) ]n = x0n + n · x0n-1( x - x0 ) + Rn(x)
 definierte Restglied  Rn(x)  gilt:
 | Rn(x) | kn ( x - x0 )² .
 Was bedeutet das Ergebnis?
 b)Für das in Aufgabe  a)  definierte Restglied gilt über dem Intervall  [ -M | M ]  ( M + )  genauer
 
| Rn(x) | n ( n - 1 )
      2		 · M n-1 · ( x - x0 )²

10.Zwei weitere Beweise der Produktenregel für Polynome
 a) Zeige: ( u + v )² - ( u - v )² = 4 u v       ( u, v ganzrationale Funktionen )
Bestätige durch Ableiten nach der Kettenregel (auf der linken Seite) die Produktenregel.
 b) 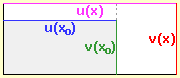Bestätige an Hand des nebenstehenden Bildes und allgemein
u (x) · v (x) - u (x0) · v (x0) = u (x0) · [ v (x) - v (x0) ] + v (x) · [ u (x) - v (x0) ]
und entwickle aus dieser Gleichung die Produktenregel.

11.Beweise die beiden folgenden Ableitungsreglen für beliebige bei  x0  differenzierbare Funktionen  f, f1, f2  (beachte Definition der L-Differenzierbarkeit).
 a) ( a · f ) ' (x0) = a · f ' (x0) b) ( f1 + f2 ) ' (x0) = f1' (x0) + f2' (x0)
 (Dabei brauchen also  f (x), f1 (x), f2 (x)  keine Polynome zu sein.)
12.Wende Ableitungsstrategien an bei
 a) f (x) = x² b) f (x) = 2 x²c) f (x) = x³d) f (x) = x4;
 c) f (x) = - 2 x² + 4 x³ d) f (x) = 4 x³ - 6 x² + 3 x + 4
13.Zeige die Anwendbarkeit der Ableitungsstrategie auch in den folgenden Sonderfällen
 a) f (x) = x b) f (x) = m x + bc) f (x) = 3d) f (x) = 0

 

weitere Aufgaben zu    6. Anwendungen I  

 zurück zu MATHEMATIK Übersicht